(L4DC 2023) Learning Global Dynamics using Koopman Operator Theory
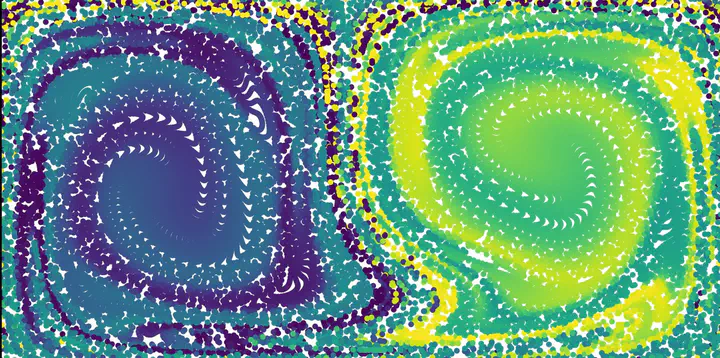Estimating the flow of non-linear dynamical systems such as the double gyre flow
Koopman operator theory states that a non-linear dynamical system can be lifted to a higher, and possibly infinite dimensional space, where the dynamics evolve linearly. Given the intractability of this infinite dimension, we develop a framework that approximates a finite set of lifting functions that linearize the system, and the respective Koopman operator.
Instead of a black-box method, or hand-selecting potential lifting functions, we characterize our lifting functions as Fourier features, and learn the optimal set of Fourier feature parameters (frequencies and phase shift) and Koopman operator for various dynamical systems of varying complexities.
Relevant Publication:
Salam, Tahiya, Alice Kate Li, and M. Ani Hsieh. “Online Estimation of the Koopman Operator Using Fourier Features.” Learning for Dynamics and Control Conference. PMLR, 2023. Link to paper.
